二进制八进制十进制十六进制之间相互转化
栏目分类:计算机知识 发布日期:2019-09-24 浏览次数:次
上一节我们了解了进制,知道常见的进制有二进制,八进制,十进制,十六进制,是不是很想知道他们是怎样转换的呀,这一节我们就学习这几个进制是怎样转换的。
上一节我们知道:
十进制就是逢十进一,十进制只能用0,1,2,3,4,5,6,7,8,9这十个数字表示,如29。
何为十六进制?
所谓十六进制就是逢十六进一,十六进制只能用0~9,A,B,C,D,E,F表示,如十进制中的29,在十六进制中表示为1D。
下表给出了0到20各进制的表示方法:
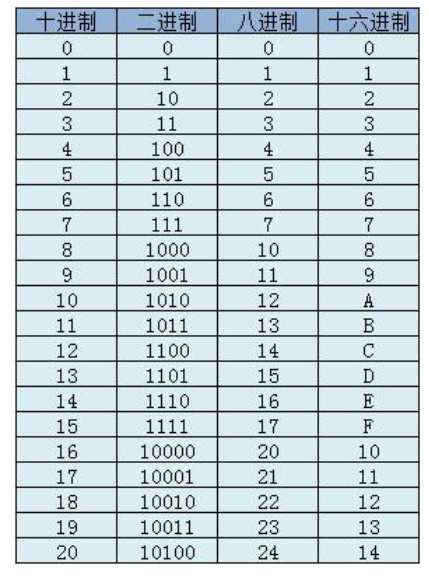
是不是看完上面的图,已经迫不及待了呀,先别着急我们先去了解两个概念:基数,位权。
基数:数制所使用数码的个数。例如,二进制的基数为2;十进制的基数为10。
位权:数制中某一位上的1所表示数值的大小(所处位置的价值)。例如,十进制的123,1的位权是100,2的位权是10,3的位权是1。
通过对上述概念的了解,我们发现十进制是以10为基数的数字系统,即它由0、1、2、3、4、5、6、7、8、9这十个基本数字组成,超过“9”这个最大的十进制基本数字之后,变成进位,即“逢十进一”。
这样,我们可以将一个十进制数按权展开得到的多项式,例如十进制数字123.4,我们可以将其描述为:
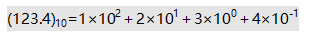
我们发现,位权是基数的整数幂。

现在我们已经了解了一些基本的进制知识,现在我们正式开始去学习进制转换
一,其他进制转化十进制
(1) 二进制数转换为十进制数
二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……
有一二进制10 0100,转换为10进制为:
计算过程:
0*2^0 + 0 * 2^1 + 1 * 2^2 + 0 * 2^3 + 0 * 2^4 + 1 * 2^5 = 36
(2) 八进制数转换为十进制数
一个八进制数:1507,转换为十进制为:
7 * 8^0 + 0 * 8^1 + 5 * 8^2 + 1 * 8^3 = 839
(3) 十六进制数转换为十进制数
一个十六进制数2AF5换算成10进制:
 =10997
=10997
这里F = 16 A = 10;
二,其他进制转二进制
(1) 八进制转二进制 31
1---->001
3---->011
这里要注意一个八进制的数要转换三位数二进制不足补零(按照第一张片)
然后我们将结果按从下往上的顺序书写就是:11001,那么这个11001就是八进制31的二进制形式
(2) 十进制转二进制 53

这就是11001就是十进制53的二进制形式
(3) 十六进制转二进制 31
1---->0001
3---->0011(跟八进制相似)
这里要注意一个十六进制的数要转换四位数二进制不足补零(按照第一张片)
然后我们将结果按从下往上的顺序书写就是:110001,那么这个110001就是十六进制31的二进制形式
上一节我们知道:
十进制就是逢十进一,十进制只能用0,1,2,3,4,5,6,7,8,9这十个数字表示,如29。
何为十六进制?
所谓十六进制就是逢十六进一,十六进制只能用0~9,A,B,C,D,E,F表示,如十进制中的29,在十六进制中表示为1D。
下表给出了0到20各进制的表示方法:

是不是看完上面的图,已经迫不及待了呀,先别着急我们先去了解两个概念:基数,位权。
基数:数制所使用数码的个数。例如,二进制的基数为2;十进制的基数为10。
位权:数制中某一位上的1所表示数值的大小(所处位置的价值)。例如,十进制的123,1的位权是100,2的位权是10,3的位权是1。
通过对上述概念的了解,我们发现十进制是以10为基数的数字系统,即它由0、1、2、3、4、5、6、7、8、9这十个基本数字组成,超过“9”这个最大的十进制基本数字之后,变成进位,即“逢十进一”。
这样,我们可以将一个十进制数按权展开得到的多项式,例如十进制数字123.4,我们可以将其描述为:
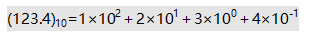
我们发现,位权是基数的整数幂。

现在我们已经了解了一些基本的进制知识,现在我们正式开始去学习进制转换
一,其他进制转化十进制
(1) 二进制数转换为十进制数
二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……
有一二进制10 0100,转换为10进制为:
计算过程:
0*2^0 + 0 * 2^1 + 1 * 2^2 + 0 * 2^3 + 0 * 2^4 + 1 * 2^5 = 36
(2) 八进制数转换为十进制数
一个八进制数:1507,转换为十进制为:
7 * 8^0 + 0 * 8^1 + 5 * 8^2 + 1 * 8^3 = 839
(3) 十六进制数转换为十进制数
一个十六进制数2AF5换算成10进制:
这里F = 16 A = 10;
二,其他进制转二进制
(1) 八进制转二进制 31
1---->001
3---->011
这里要注意一个八进制的数要转换三位数二进制不足补零(按照第一张片)
然后我们将结果按从下往上的顺序书写就是:11001,那么这个11001就是八进制31的二进制形式
(2) 十进制转二进制 53

这就是11001就是十进制53的二进制形式
(3) 十六进制转二进制 31
1---->0001
3---->0011(跟八进制相似)
这里要注意一个十六进制的数要转换四位数二进制不足补零(按照第一张片)
然后我们将结果按从下往上的顺序书写就是:110001,那么这个110001就是十六进制31的二进制形式
本文由IT教学网整理发布,转载请注明出处:http://www.itjx.com/rumen/jisuanji/486.html

